
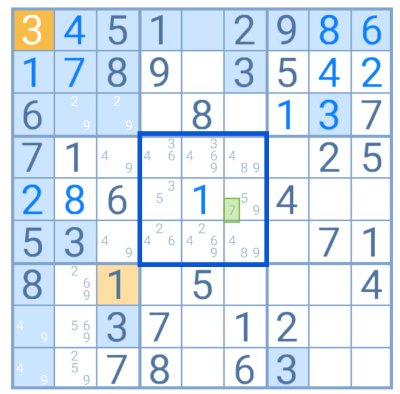
array fieldBounds ) ( mapM ( uncurry ( fmap. Node sudoku ( chooseMinLen ( map ( map treeAltToStandardOptimize ) subs )) maybeComplete :: T -> Maybe Complete maybeComplete sudoku = fmap ( Array. treeAltToStandardOptimize :: ATree T -> Tree T treeAltToStandardOptimize ( ANode sudoku subs ) = let chooseMinLen = chooseMinLen xs = minimumBy compareLength xs in Tree. This does a backtracking search, trying possibilities until it finds one which works, and backtracking when it can no longer make a legal move. It possibly looks even more naïve than it actually is. 17 Constraint Propagation (a la Norvig).Additionally, the green cells two pencil marks must appear in each of the blue. If you ask me, 'V Wing' is more appropriate In order for this to work, the cell in the middle of the 'Y' (green) must intersect both of the cells on its wings (blue), while the two wing cells may not intersect each other. 7 Very smart, with only a little guessing XY Wing is sometimes just called 'Y Wing'.Good luck! By looking for cells with few combinations throughout a puzzle and working out what that must mean for the rest of the puzzle, you will have taken an important step towards successfully solving a killer sudoku puzzle. Similarly we can place a '4' in the bottom right for the same reason. But since we know the '2' for the row must be in cell one or two, we know that it must be '6', and thus we mark it accordingly, and also write in the '3' at the right edge as that's the only possible value left for that cell. It can't be '4', '4' (repetition) therefore it must be '6' and '2'. We now know the '8' cannot contain a '5' as the '5' is already placed in the 3 x 2 now. Therefore this square must contain a '5'! Thus we place it, and move the cursor to the '8', as we are about to place that next! But it cannot contain a '3' because then the sum for '6' would be 3, 3 which is against the rules. But we can go further! The cell containing the '6' cannot contain a '6', meaning it must contain a '3' or '5'. Therefore we know that the three empty cells at the right of the row must contain one of 3,5,6. Now, we know the 1,2,4 are placed in the first three cells of the row. Let's carry on from where we were, and show the rest of the row that contains the '4' we have now placed: Once you have used the second rule to place a number, apply it again! Here's an example of how powerful this technique is. This is probably the logical technique combined with rule application you will use most often in killer sudoku - for instance once you know the cells where a number must go in a row or column even if you cannot isolate exactly which, you then know it cannot go anywhere else in that row or column. We can now apply the rule that each 3 x 2 must contain 1 - 6 once exactly to place the top right value with certainty - it must be a '4'. Now despite not knowing exactly where the 1,2,3,5,6 go in this 3 x 2 square, we know that those five cells must contain those numbers in some order.
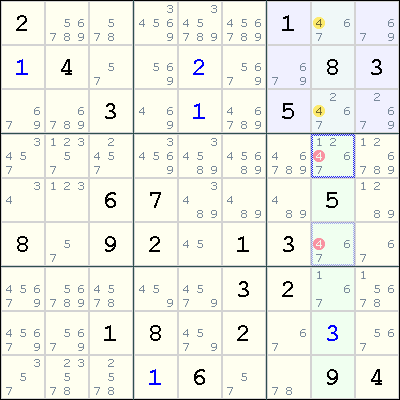
We know that this can only be composed of 6, 5, 3, so let's mark that accordingly on the grid: We see a run of '14' composed of three cells. Emeritus Professor of Mathematics Jerry Janusz presents a survey, step-by-step, of most of the known techniques used in solving Sudoku puzzles and illustrates them with many examples so that the casual solver may learn to complete some of the 'hard. Let's see this here by applying the first rule to the bottom left of the example. 16.95 12 Used from 6.40 12 New from 16.95. (Pity there is no eliminations in row G). The pattern is perfectly correct for an X-Wing in the columns eliminating in the rows. But if you look at cells G7 and G8 you can make an X-Wing with C7 and C8 on 8. Often you don't need to know where a number goes for sure to work out what another number must be. The first strategy used is Pointing Pairs using cells C7 and C8 - removing 8 in C2. This gives us:Ģ - Use your pencilmarks to deduce values elsewhere We know this must be '2' and '1' or '1' and '2', so mark it accordingly using pencil marks. Here we can see there is a '3' composed of two cells. In this example we use parts of a 3 x 2 puzzle, therefore the numbers used are from 1 to 6. The best way to get started is to look for the cells that can have the least possible values from the start. And no starting numbers are given to help you out! Here are some strategies to use to solve the puzzle:ġ - Look for cells with the least combinations However the twist is the grid is split into various shapes, and for each shape a number is given which corresponds to the sum of the cells that compose that shape. All the rules remain in place with regard the rows, columns and 3 x 2 or 3 x 3 squares containing the numbers 1 - 6 or 1 - 9 once and once only. Killer Sudoku is a fun variant of the standard sudoku puzzle.


 0 kommentar(er)
0 kommentar(er)
